主にダイナミックに変動する現象や時系列データに関する数理的研究を行っています．以下に例を挙げます．
キーワード：ニューラルネットワーク，リザバーコンピューティング，時系列パターン認識，機械学習，人工知能，データサイエンス，脳型計算，
非線形システム，数理モデリング，複雑系科学，複雑ネットワーク，力学系理論，分岐理論，相転移，最適化アルゴリズム，制御理論，数理生物学
機械学習による時系列パターン認識
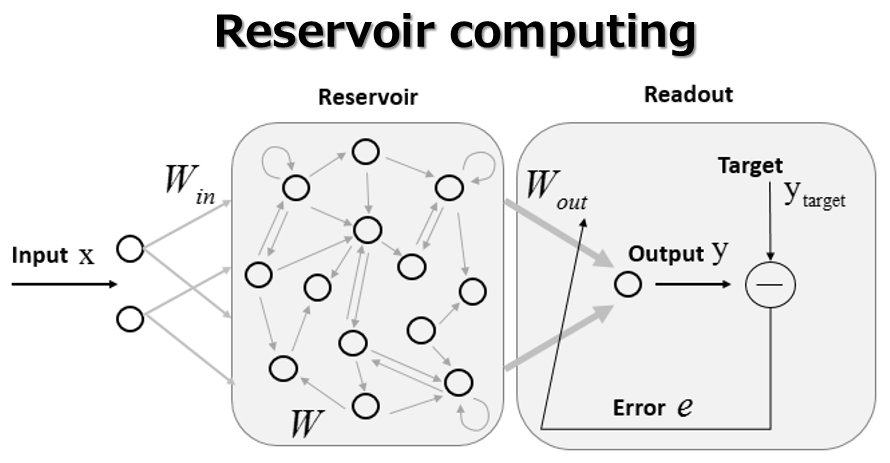
時間とともに変動する（履歴をもつ）データを時系列データと言います．音声，気象，生体信号，株価のような時系列データの情報処理を行うための数理的研究を行っています．とくに，リザバーコンピューティングという機械学習手法に基づく時系列パターン認識技術の開発に重点的に取り組んでいます．
・書籍：リザバーコンピューティング（森北出版, 2021）
・解説：リザバーコンピューティングの概念と最近の動向（電子情報通信学会論文誌, 2019）
・キーワード解説：リザバーコンピューティング（映像情報メディア学会誌, 2020）
脳型計算の数理的研究
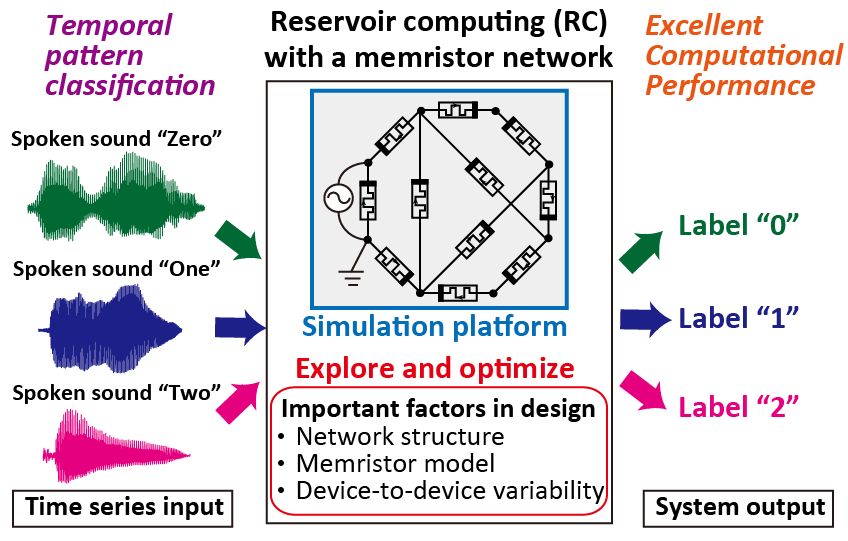
脳は少ないエネルギーで柔軟な情報処理を行っています．その仕組みにヒントを得て，高効率な脳型計算モデルの構築に取り組んでいます．また，省エネな脳型計算ハードウェアの実現に向けた数理的研究も行っています．
・論文：物理リザバーコンピューティングの包括的レビュー（Neural Networks, 2019）
・論文：省エネルギー連想記憶ニューラルネットワーク（IEEE TNNLS, 2020）
・論文：ニューロモルフィック計算のロードマップ（Neuromorph. Comp. Eng., 2022）
複雑現象の数理モデリング
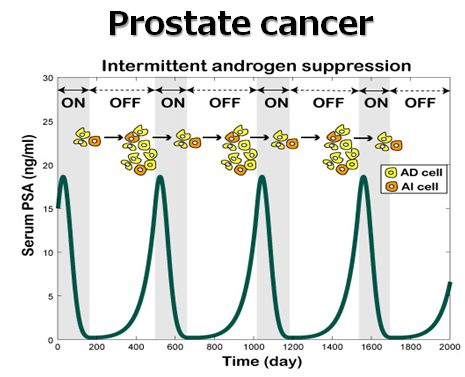
実世界には支配原理が十分に明らかではない複雑系がまだ数多くあります．数理モデリング技術を駆使して，複雑系を理解するための研究を行っています．とくに疾病・公衆衛生・医療などに関わる実現象の理解を通じて，有効な対策・介入を提案することを目指しています．
・論文：感染症抑制のための選択的介入の有効性 (Sci. Rep., 2014)
・解説：細胞システムの動態と分岐理論 (生物物理，2016)
・論文：前立腺がん間欠治療の数理モデリング (Phil. Trans. Roy. Soc. A, 2010)
ネットワーク動的頑強性
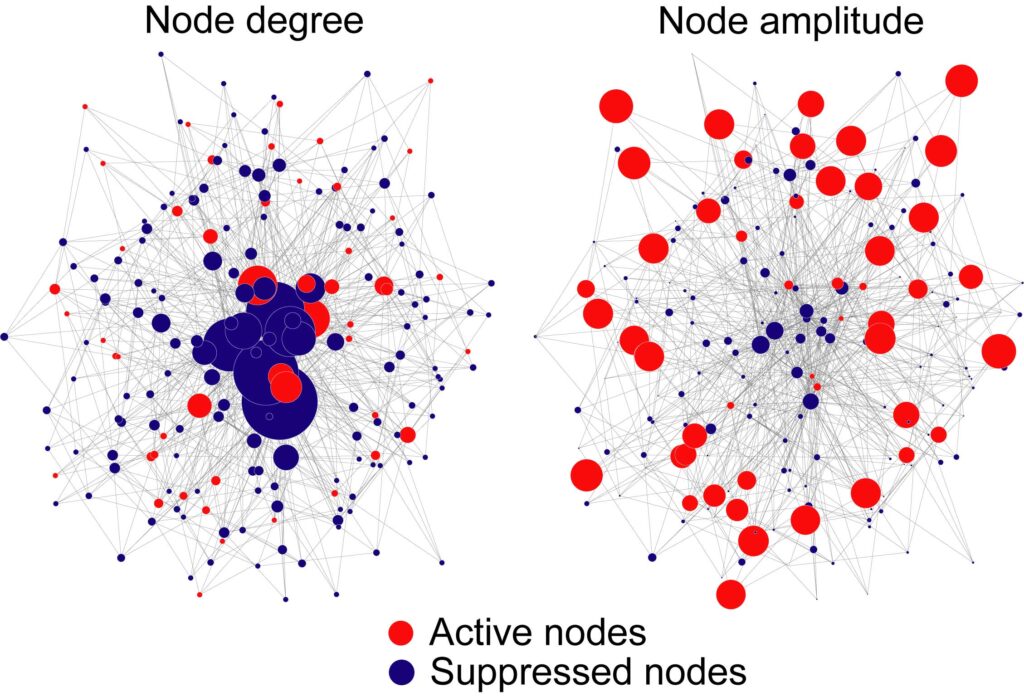
複雑なネットワークシステムは，電力網，交通網，生体網など，至るところに見られます．ネットワーク化によって通常時の利便性は向上しますが，一部の故障が全体に波及して被害を拡大するというリスクも生じます．ネットワーク上の動的プロセス（伝播や流れ）がある場合について，ネットワークシステム機能の動的頑強性を調べるための数理的研究を行っています．
・招待講演論文：複雑ネットワークの動的頑強性 (IEICE, CCS, 2018)
・論文：複雑ネットワークの動的頑強性－低次数ノードの重要な役割－ (Sci. Rep. 2012)
複雑系動力学の基礎理論
動的システムの挙動の定性的変化や複雑化のプロセスを理解するための基礎数理的研究を行っています．同じ物質やシステムでも，環境や条件が変化すれば，その振る舞いは単純から複雑へ，秩序から無秩序へ，また規則から不規則へ，と定性的変化を示すことがあります．その時間的・空間的複雑化が生じるメカニズムを非線形力学系理論や相転移理論をもとに探求しています．
・チュートリアル：２次元写像系の間欠カオスとそのメカニズム (SIAM DSweb, 2005)