The main topics are mathematical studies on dynamical phenomena and temporal data. Examples are found below.
Keywords:Neural networks, Temporal pattern recognition, Reservoir computing, Machine learning, Artificial intelligence, Data science, Neuromorphic computing,
Nonlinear dynamics, Mathematical modeling, Complexity science, Complex networks, Dynamical systems theory, Bifurcation theory, Phase transition,
Optimization algorithms, Control theory, Mathematical biology
Temporal pattern recognition with machine learning
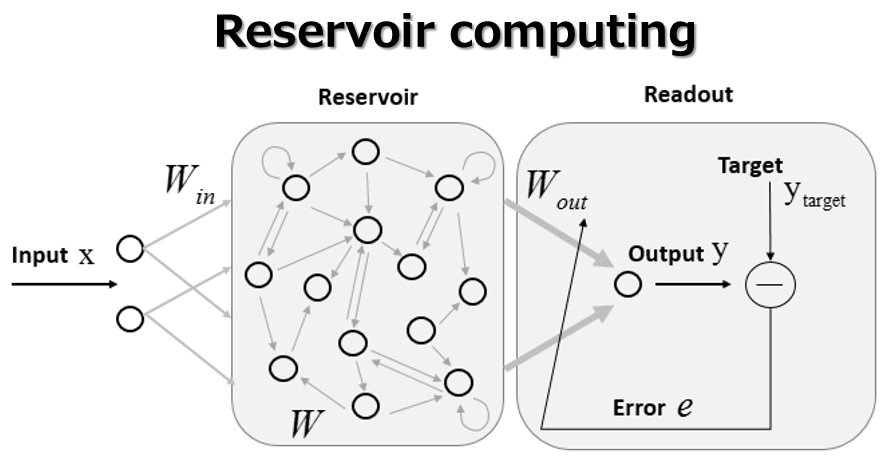
Time series data indicates data varying with time. We conduct mathematical research on information processing of time series data such as sounds, climates, and biological signals. In particular, we have been focusing on development of temporal information processing techniques based on reservoir computing.
・[Book (in Japanese)] Reservoir Computing(Morikita publishing, 2021)
・[Editorial] Special Issue on New Frontiers in Extremely Efficient Reservoir Computing (IEEE TNNS, 2022)
Mathematical studies on
brain-inspired computing
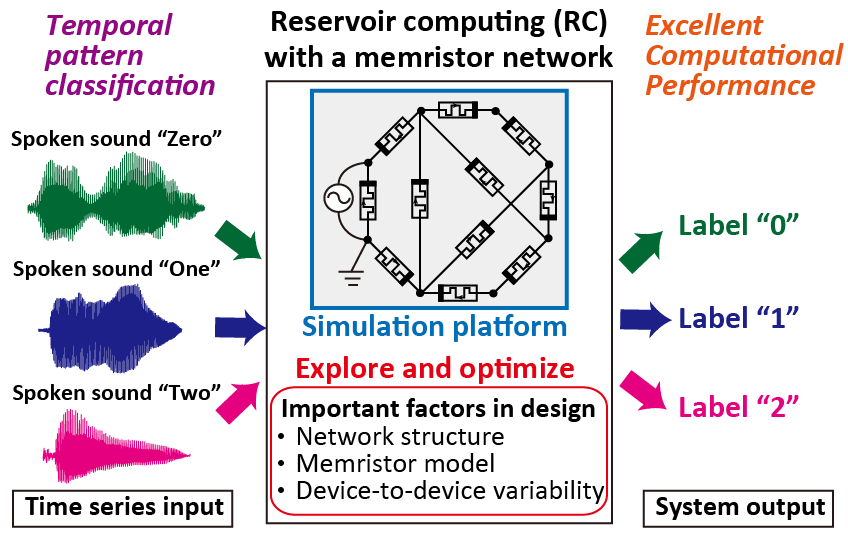
Biological brains realize flexible information processing with extremely low energy. By imitating the mechanism of the brain, we are constructing efficient brain-inspired computing models. We are also conducting mathematical studies on energy-efficient brain-inspired computing hardware systems.
・[Paper] A review on physical reservoir computing(Neural Networks, 2019)
・[Paper] Energy-efficient neural associative memory(IEEE TNNLS, 2020)
・[Paper ]2022 Roadmap on neuromorphic computing and engineering(2022)
Mathematical modeling of
complex phenomena
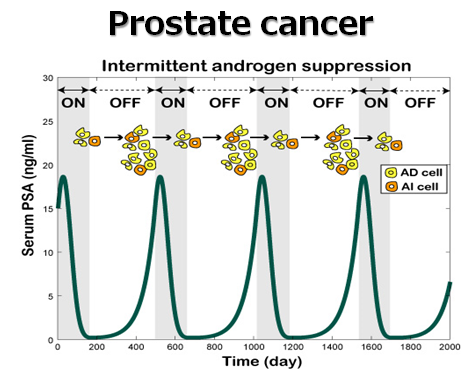
There are a lot of complex phenomena in the real world, whose governing rule is not fully clear. We are conducting research on understanding complex systems by using mathematical modeling techniques. In particular, we focus on various phenomena related to diseases, public health, and medicine for proposing effective measures and intervention.
・[Paper] Random and targeted intervention for epidemic control (Sci. Rep., 2014)
・[Paper] Atopic dermatitis (J. Theor. Biol., 2018)
・[Paper] Prostate cancer under hormone therapy (Phil. Trans. Roy. Soc. A, 2010)
Network robustness
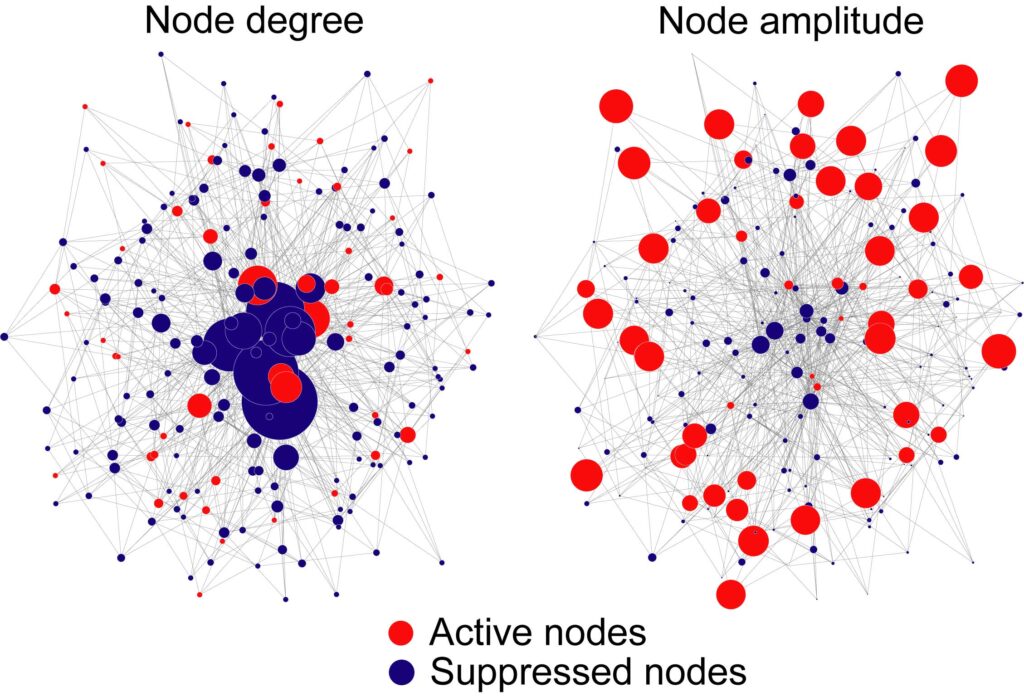
Network systems are ubiquitous as found in power, traffic, and biological networks. Networking is beneficial in normal situations, but it poses a risk that a failure in a small part of the network causes a breakdown of the whole system. We are conducting mathematical studies on the robustness of dynamical processes on complex networks.
・[Paper] Dynamical robustness of complex networks (Sci. Rep., 2012)
・[Paper] Dynamical robustness of coupled heterogeneous oscillators (PRE, 2014)
Fundamental theory of complex systems dynamics

We are conducting fundamental mathematical studies to understand the process of qualitative changes in dynamical systems. A dynamical system changes its behavior from simple to complex, from order to disorder, and from regular to irregular, depending on the variation of environments. We are interested in clarifying how such spatial and temporal complication occurs in terms of bifurcation and phase transition.
・[Tutorial] Crisis-induecd intermittency in 2D coupled maps (SIAM DSWeb, 2005)
